本記事では「高専の数学」について解説しています。
5年制の理工系専門教育機関である高専。
入学する以上、切っても切れない関係となるのが数学の授業です。
「ついていけるのかな…。」「どれくらいのスピードで進むのかな？」と、不安に感じる人は多いのではないでしょうか。
本記事では「高専で学ぶ数学の内容」だけでなく、「進度」「得意になる方法」まで詳しく解説しています。
高専OBによる1記事で、不安や疑問が解消されるはずですよ。
- 数学を学習する目的を知りたい人
- 数学を通して「求められる能力」を知りたい人
- 高専への適性を知りたい中学生
- 数学を得意にするための勉強法を身につけたい人
「高専ってそもそもどんな学校？」という方は以下の記事もおすすめです。
さっそくみていきましょう。
┄MENU┄
高専で数学が重視される理由2つ
以下からは高専において数学が重視される理由と、求められる能力を深掘りしていきます。
①論理的思考力を養うため
機械工学・電気工学・情報工学・土木工学などの専門分野は数字無くして語れません。
なぜなら言葉の代わりに数字を使う、といっても過言ではないからです。
例えば、モノを作りたい場合。
プロセスにおいて、モデリングやデータ解析、規格管理の設計など多くの場面で具体的な数値は必須です。
数値と複合した知識を合わせて、ようやくモノが完成するのです。
論理的思考を確立させるには数学と技術を複合した知識が絶対といえるでしょう。
特にエンジニアを目指す人は必須ですよ。
②最新技術を理解するための基礎
最新技術を理解するためには、基礎からの数学が重要になります。
現代の機械やシステムは技術革新のため高度化し、新しい技術や理論が次々と登場。
使いこなすためには、過去からの工程を理論立てて理解したうえで、応用する力が求められます。
そのため、最新技術の前に基礎を抜かりなく理解しておく必要があるのです。
高専で習う数学
専門的なレベルを目指すために、数学は必須科目。
一般的に高専では、下記のような順番で数学を学んでいきます。
| 学年 | 内容 | 詳細 |
| 1年生 | ・数と式 ・方程式と不等式 ・関数とグラフ ・図形と計量（幾何） | 中学校の復習と高校数学の基礎。 |
| 2年生 | ・三角関数 ・指数関数と対数関数 ・微分と積分の基礎 ・数列と級数 | ・高校数学の発展。 ・2年生で高校数学を修了。 |
| 3年生 | ・微分法と積分法の応用 ・多変数関数 ・行列とベクトル ・線形代数の基礎 | ・大学レベルの内容へ。 ・難易度up！ ・数式や図形のイメージが難しい。 |
| 4年生 | ・高等微分積分学 ・常微分方程式 ・複素関数論 ・確率と統計 | ・より専門的な内容・応用数学に突入。 |
| 5年生 | ・応用数学（工学、情報、物理などに関連） ・フーリエ解析 ・数学的モデリング | ・各研究や分野に特化した数学へ。 |
個人的に難しかったのは「4年生」。
難易度が一気に上がり、ついていくのが大変でした。
つまずきやすいポイント3選
高専の数学はハイペースで進んでいくため、つまずきやすいポイントがたくさん。
以下からは、高専OBの筆者が特に苦労したポイントを解説していきます。
①三角関数（2年生）
数字を扱う教科なのに、記号と世界観が登場する「サイン・コサイン・タンジェント（sin、cos、tan）」
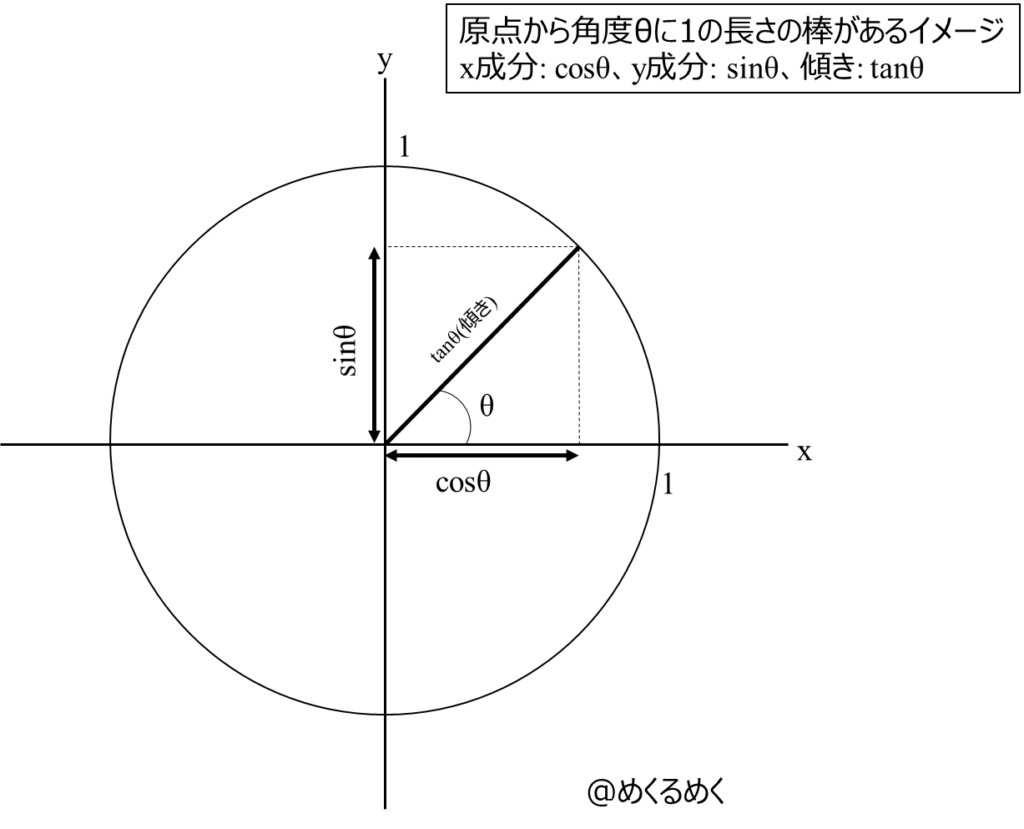
「ある長さの棒が原点からの角度で伸びている時、縦と横の2つの成分に分解される」
…と想像して乗り切りました。
以下の図のような半径1の円をイメージするとわかりやすいです。
②微分と積分（2～5年生）
「dx」という微小な幅の面積を求め(積分)、分解（微分）する分野です。
微分積分にはイメージが大事。
グラフの面積を積み重ねる「積分」と特定の幅の傾きを表す「微分」と、それぞれ想像すると分かりやすいです。
微積分を通して、今までとは次元が違う数学へ変化していきます。
（例えば、距離⇔速度⇔加速度など）
対数関数（3年生）
掛け算の上位互換の「log」という概念が追加されます。
乗数の逆をするのですが、イメージが難しいことに加え、エクスポネンシャルeと組み合わさり、応用のレベルが高いです。
グラフや図を使って視覚的に理解すると、分かりやすくなります。
高専の数学に関する質問3選
以下からは、高専の数学に関係する疑問3つをピックアップして解説していきます。
数学が苦手な人は高専に入れない？
数学が苦手だと、高専に入学できたとしても通い続けることが難しいです。
高専では、1～3年生のおよそ24％が数学の授業。
進度が速い上に、カリキュラムは大学数学をも含みます。
また、卒業後は就職先での即戦力にもなり得るため、根本から理解し技術を扱えるレベルへの到達が求められるのです。
そのため数学に苦手意識を持つ人は、「入る」ことはできても「続ける」ことが困難でしょう。
車の知識だけは誰にも負けないような知人がいたのですが、彼は数学が苦手。
結果的に留年し、そのまま退学してしまいました…。
数学が得意になるには？
数学を得意にする秘訣は「想像力を活かすこと」、「できない部分を放置しないこと」2つです。
高専での数学は一度つまずいてしまうと、以降の応用までドミノ倒しでできなくなる場合がほとんど。
そのため、つまずいた部分をしっかりと振り返り、苦手でも「理解を促す」必要があります。
また、学習する際に重要になるのが想像力です。
数字だけで考えるのでなく、図形や物理現象などに照らし合わせると格段に理解しやすくなります。
筆者は、自分なりに連想や図を描いていました！
中学校の数学はどれぐらい使う？
中学校で習う内容は、高専での数学において基礎的な考え方になります。
特に中学校の関数や図形に関する知識は、高専5年生まで活用していきます。
そのため苦手な箇所がある場合、入学前に理解しておくとスムーズに始められるでしょう。
高専の数学は難しい？ まとめ
本記事では「高専の数学は難しい？進度・カリキュラム・得意になる方法まで！」を解説してきました。
- 「論理的思考」「最新技術の理解」に数学は必要
- 数学が苦手だと、入学できても通い続けることが困難
- 数学を得意にするには「想像力」「苦手を放置しないこと」が大事
- 中学数学は関数や図形に関する知識が特に必要
高専数学に対して不安がある方の疑問解消につながれば嬉しく思います。
最後まで読んでいただきありがとうございました。
